
Lineare Funktionen Aufgaben Mit Lösungen Klasse 9 Pdf Lineare Gleichungen Arbeitsblatt 3738
Die vorliegenden Extremwertaufgaben sind Textaufgaben, meist mit Zeichnungen versehen, bei denen die Frage gestellt wird, unter welchen Bedingungen ein Wert (z.B. Abstand, Länge, Fläche, Volumen) am größten oder am kleinsten ist.

Extremwertaufgaben, Blechverbrauch minimal? (Mathe)
Übungsaufgaben zu Extremwertprobleme. Lösungen. zu 1: Bei einem Rechteck mit den Seitenlängen x und y gilt für die Umfangslänge: u = 2⋅(x + y) Mit u = 8. ⇒. 2⋅(x + y) = 8, also x + y = 4 und damit y = 4 - x. Weiter gilt für den Flächeninhalt A des Rechtecks:

Extremwertaufgaben Mit Lösungen Pdf
3 Ein Rechteck soll mit 16 m Zaun eingefasst werden. An der Hauswand ist kein Zaun nötig. Wie groß kann die Fläche maximal werden? Term: A= l⋅b Nebenbedingungen: l 2b = 16 Definitionsbereich: l∈[0;16] , b∈[0; 8] Zielfunktion: A b = l⋅b = 16−2b ⋅b = 16b−2b2 = −2b2 16b Extrema: Die Funktion und alle benötigten Ableitungen:

Extremwertaufgaben 3 Flächeninhalt für "schwieriges" Rechteck, Teil 2 Optimierung YouTube
Theorie und Lösungsmethoden für Extremwertaufgaben anwenden zu können. Ab-schließend ist jedoch zu überprüfen, ob die so erhaltenen Lösungen die Nicht-Negati-vitätsbedingungen erfüllen. Beispiel 19.1: Betrachtung mathematischer Modelle für Extremwertaufgaben, die bereits Einsatzmöglich-keiten in der Wirtschaft erkennen lassen:

Aufgaben Extremwertaufgaben mit Lösungen Koonys Schule 1597
Mit der Differentialrechnung ermitteln wir den Extremwert: x = 5 und den maximalen Fl ̈achen-inhalt A = 50 (Zwischenergebnis: A′(x) = 20 − 4x). Zur L ̈osung von Extremwertaufgaben sind im allgemeinen folgende Schritte durchzuf ̈uhren: Skizze mit Bezeichnungen der Variablen anfertigen,

Sicheres Wissen und Können. Ebene Geometrie. Sekundarstufe I PDF
Meistens haben Extremwertaufgaben zwei Teile. Der erste Teil besteht aus einer Formel, die meist mehr als nur eine abhängige Variable hat. Im zweiten Teil bekommt man mehr Informationen, die sich auf den ersten Teil beziehen. Damit kann man die Formel so umschreiben, dass man nur noch eine einzige abhängige Variable hat.
eFunktion Kurvendiskussion, Geradengleichungen, Flächen, Extremalprobleme Mathe Test mit
7 Extremwertaufgaben mit Funktion als Nebenbedingung Siehe dazu den Abschnitt 11.3 in der Formelsammlung. 7.1 Aufgaben Gegeben ist die Funktion f mit (x) = − x + 4 deren Graph zusammen mit dem Intervall [0 ; 8] der x-Achse und [0 ; 4] der y-Achse ein Dreieck bildet.

Extremwertaufgaben mit Nebenbedingungen RAAbits Online
Ein Hochregallager mit einem Gesamtvolumen von 500m3 soll m oglichst kosteng unstig hergestellt werden. Dabei schlagen die W ande mit 1000 e je m2, die Decke mit 600e je m 2sowie der Boden mit 400e je m zu Buche. Welche Maˇe sollten verwendet werden, wenn ein quadratischer Grundriss gew ahlt wird? 3.13 Aufgabe 13 b
Maximalen Flächeninhalt berechnen Analysis SchulLV
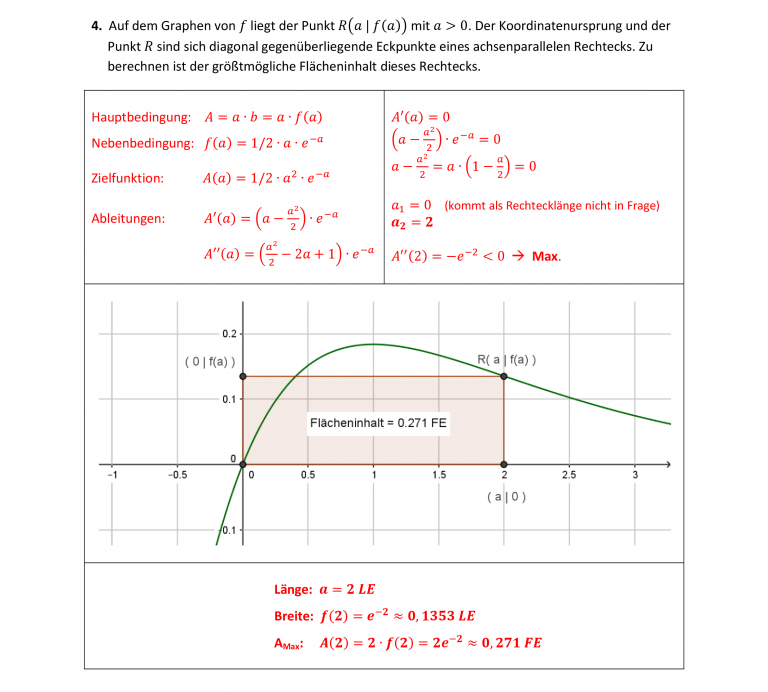
Eine Extremwertaufgabe ist ein Aufgabentyp, bei der zu einer Problemstellung die optimale, d.h. maximale oder minimale Lösung gesucht wird. In diesem Abschnitt lernst du ein Rezept kennen, wie du eine Extremwertaufgabe formulierst und sie löst. Gegeben ist die Funktion mit . Sei ein Punkt auf dem Graphen von mit .

Extremwertaufgaben 1 Beispiel für Flächeninhalt Dreieck maximieren (aka Optimierung) YouTube
6.1 Aufgaben mit quadratischen Funktionen (Lösungen) 1. Mit den Rechteckseiten a und b gilt für die Ausgangsgleichung und Nebenbedingung A(a,b) = ab bzw. U = 2a+2b = 16km. Die Nebenbedingung nach a umstellen ergibt a = 8km − b und eingesetzt in die Ausgangsglei-chung A(b) = (8km−b)b = −b2 +8kmb und damit die Ableitungen

Schwere Matheaufgaben Für Lehrer Mit Lösung Aufgaben Mathematikunterricht Gute
Lösungen: 1) Das Volumen ergibt sich durch V = x2y und die Oberfläche besteht aus dem Einfachen (da vorne offen) der Grundfläche, also x2 und den 4 rechteckigen Seitenflächen mit den Maßen x und y, womit für die Oberfläche O = x2 + 4xy gilt. Damit ergibt sich folgendes: min. O = x2 + 4xy NB: x2ÿy = 4000 Wir lösen die NB nach y auf (y = 4000/x2 (1)) und setzen diese in die Zielfunktion.
1.5.7 Extremwertaufgaben Abiturskript
Eine Extremwertaufgabe ist eine Fragestellung, bei der du eine Größe unter bestimmten Bedingungen maximieren oder minimieren sollst. Diese Größe hängt dabei von Variablen ab, an welche häufig bestimmte Bedingungen - die sogenannten Nebenbedingungen - geknüpft sind.

Sekundarstufe Unterrichtsmaterial
Zeige mit einer sauberen Zeichnung, dass P der Fußpunkt des Lotes von A auf die Gerade g ist. Mathematik * Jahrgangsstufe 9 * Extremwertaufgaben * Lösungen 1. F a b a(20cm a) hat den größten Wert für a b 10cm. Der maximale Flächeninhalt beträgt also 100cm2. 2. a) y 1,5x 6 b) P(x / 6 1,5x ).

www.mathefragen.de Extremwertaufgaben
1. Aus einem Blech der Länge a und der Breite b soll eine Dachrinne (der Länge a) hergestellt werden, die maximales Wasservolumen aufnehmen kann. a) Die Dachrinne wird V-förmig gebogen. Welcher „Knickwinkel" ist zu wählen? Welches maximale Volumen ergibt sich? a) b) Die Dachrinne wird rechtwinklig gebogen. Welches maximale Volumen ergibt sich?

Extremwertaufgaben Übungen Mit Lösungen Pdf 2023
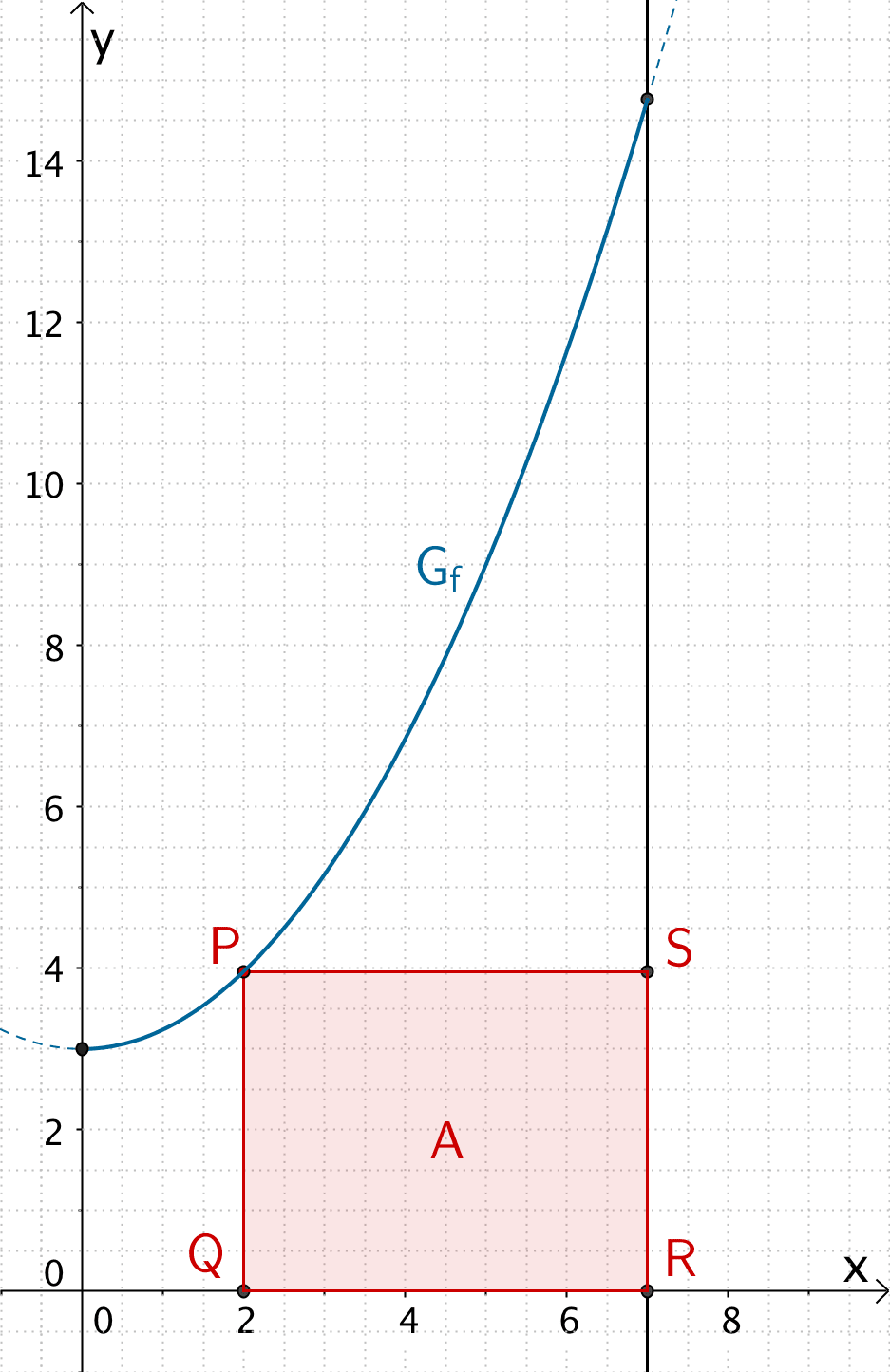
4. Gegeben ist die Funktion f(x) = −4x² + 144. f begrenzt mit der x-Achse eine Fläche, der ein Dreieck ABC eingeschrieben wird. Die Punkte A und B liegen auf der x-Achse, A auf dem Schnittpunkt von f mit der x-Achse, C liegt auf dem Graphen von f. Berechnen Sie, für welchen Wert das Dreieck einen maximalen Flächeninhalt hat!

Extremwertaufgaben mit Nebenbedingungen RAAbits Online
Lösungen: 1) Das Volumen ergibt sich durch V = x2ÿy und die Oberfläche besteht aus dem Einfachen (da vorne offen) der Grundfläche, also x2 und den 4 rechteckigen Seitenflächen mit den Maßen x und y, womit für die Oberfläche O = x2 + 4xy gilt. Damit ergibt sich folgendes: min. O = x2 + 4xy NB: x2ÿy = 4000 Wir lösen die NB nach y auf (y = 4000/x2 (1)) und setzen diese in die.
